주성분 분석(PCA)이란?
오늘은 가장 인기있는 차원 축소 알고리즘인 주성분 분석(Principle Component Analysis, PCA)에 대해서 알아봅시다.
차원의 저주란?
많은 경우 머신러닝 문제는 훈련 샘플이 각각 수천, 혹은 수백만개의 특성을 가지고 있습니다. 이렇게 특성들이 많을 경우, 유의미한 특성들을 찾기가 어려울 뿐더러 훈련을 느리게 해 결과적으로 성능 저하를 일으키는 원인이 됩니다. 이런 문제를 "차원의 저주"(curse of dimensionality)라고 합니다.
이런 경우에는 당연하게도 차원을 줄여줘야 하는데, PCA는 그 중에서도 가장 많이 사용되는 차원 축소 알고리즘입니다. PCA에 대해서 자세히 알아봅시다!
PCA (Principle Component Analysis), 주성분 분석
PCA는 말 그대로 '주' 성분을 분석하는 것입니다.
분산을 보존하자!
저차원의 초평면에 투영을 하게 되면 차원이 줄어들게 됩니다. 그럼 어떤 초평면을 선택하면 좋을까요?

위와 같은 예시를 살펴봅시다. 간단한 2D 데이터셋이 있을 때, 세개의 축을 우리의 초평면 후보로 둡시다. 여기에서 볼 수 있는 것은 실선을 선택하는 방법이 분산을 최대로 보존하는 것이고, c2의 점선을 선택하는 것이 분산을 적게 만들어버리는 방법입니다.
다른 방향으로 투영하는 것 보다 분산을 최대로 보존할 수 있는 축을 선택하는 것이 정보를 가장 적게 손실할 수 있다고 생각할 수 있습니다. 분산이 커야 데이터들사이의 차이점이 명확해질테고, 그것이 우리의 모델을 더욱 좋은 방향으로 만들 수 있을 것이기 때문입니다.
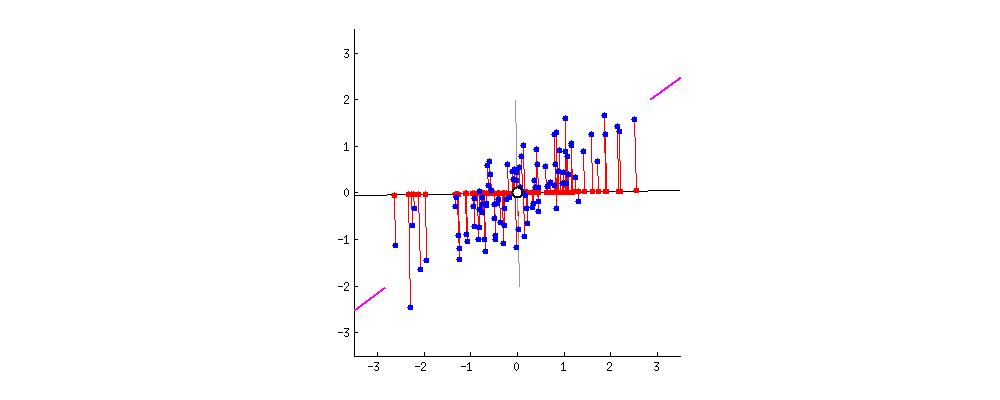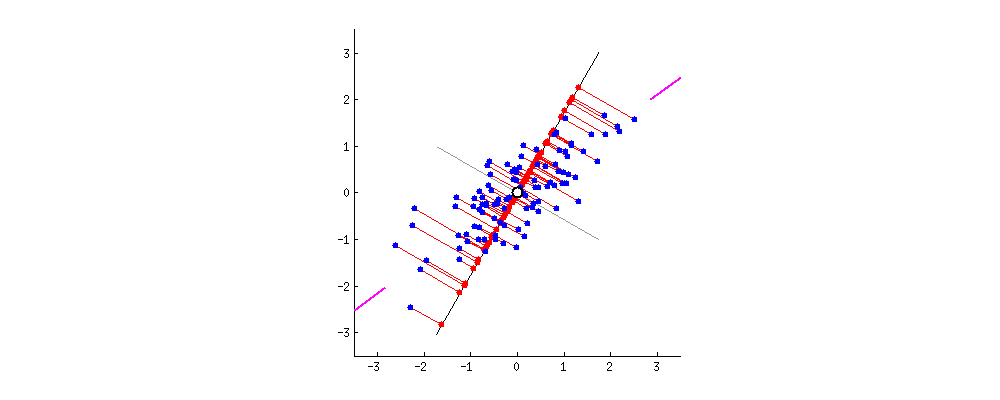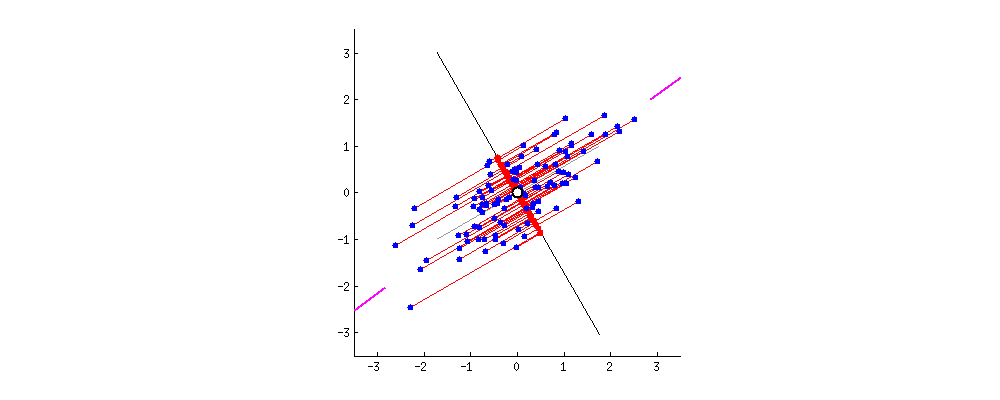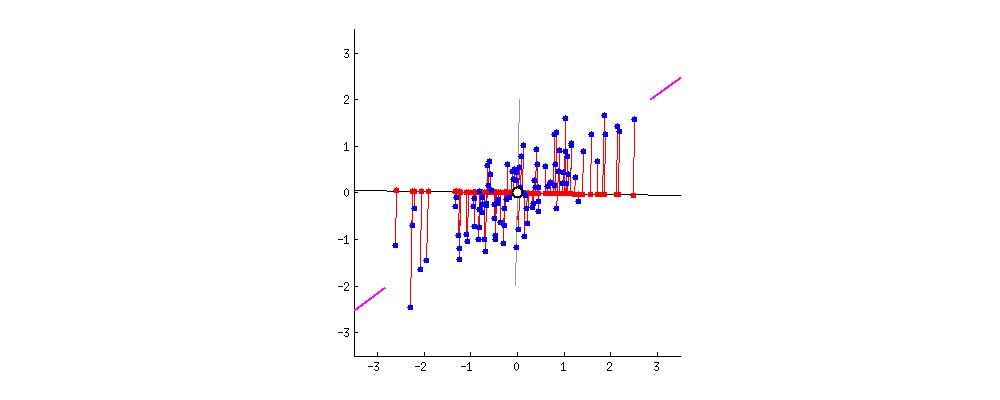
그래서 PCA에서는 분산이 최대인 축을 찾고, 이 첫번째 축에 직교하고 남은 분산을 최대한 보존하는 두번째 축을 찾습니다. 2D 예제에서는 선택의 여지가 없지만, 고차원의 데이터셋이라면 여러 방향의 직교하는 축을 찾을 수 있을 것입니다.
이렇게 i번째 축을 정의하는 단위 벡터를 i번째 주성분(principal component, PC)라고 합니다. 위 예제에서는 첫번째 PC는 c1이고, 두번째 PC는 c2입니다.
주성분을 찾는 법
특잇값 분해(Singular Value Decomposition, SVD)이라는 표준 행렬 분해 기술을 이용해 훈련 세트 행렬 X를 3개의 행렬의 점곱인 $U \cdot \sum \cdot V^T$로 분해할 수 있습니다. 여기서 우리가 찾고자하는 모든 주성분은 V에 담겨있습니다.
아래 파이썬 코드는 넘파잉의 svd() 함수를 사용하여 훈련 세트의 모든 주성분을 구한 후 처음 두개의 PC를 추출하는 코드입니다.
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]d차원으로 투영하기
주성분을 모두 추출했다면 처음 d개의 주성분으로 정의한 초평면에 투영하여 데이터셋의 차원을 d차원으로 축소할 수 있습니다. 이 초평면은 분산을 가능한 최대로 보존한 투영입니다.
초평면에 훈련 세트를 투영하기 위해서는 행렬 X와 첫 d개의 주성분을 담은(즉, V의 첫 d열로 구성된) 행렬 $W_d$를 점곱하면 됩니다.
$$ X_{d-proj} = X \cdot W_d $$
아래 파이썬 코드는 첫 두개의 주성분으로 정의된 평면에 훈련 세트를 투영합니다.
W2 = Vt.T[:, :2]
X2D = X_centered.dot(W2)여기까지 하면 PCA 변환이 완료되었습니다!
더 쉽게 PCA를 하는 방법 - 사이킷런 이용하기
사이킷런의 PCA 모델은 앞서 한 것처럼 SVD 분해 방법을 사용하여 구현합니다. 사이킷런의 PCA모댈은 자동으로 데이터를 중앙에 맞춰줘서 별도의 가공 없이 바로 사용할 수 있습니다.
from sklearn.decomposition import PCA
pca = PCA(n_components = 2)
X2D = pca.fit_transform(X)
'머신러닝 꿈나무 > 기본 개념' 카테고리의 다른 글
| 토큰화(tokenize)란? (0) | 2022.02.17 |
|---|---|
| [pyspark/빅데이터기초] Parquet(파케이) 파일 형식이란? (0) | 2021.11.17 |
| [빅데이터기초] 스파크란? (0) | 2021.11.13 |
| 켄달타우란? - 비모수적 상관계수에 대해서 (0) | 2021.05.24 |
| 맥북에서 딥러닝 개발환경 구축하기 - 아나콘다, oh-my-zsh, iterm2, jupyter lab 테마 설정하기 (0) | 2021.01.13 |
댓글
이 글 공유하기
다른 글
-
[pyspark/빅데이터기초] Parquet(파케이) 파일 형식이란?
[pyspark/빅데이터기초] Parquet(파케이) 파일 형식이란?
2021.11.17 -
[빅데이터기초] 스파크란?
[빅데이터기초] 스파크란?
2021.11.13 -
켄달타우란? - 비모수적 상관계수에 대해서
켄달타우란? - 비모수적 상관계수에 대해서
2021.05.24 -
맥북에서 딥러닝 개발환경 구축하기 - 아나콘다, oh-my-zsh, iterm2, jupyter lab 테마 설정하기
맥북에서 딥러닝 개발환경 구축하기 - 아나콘다, oh-my-zsh, iterm2, jupyter lab 테마 설정하기
2021.01.13