[Algorithm] DFS와 BFS 기본 개념 및 관련 문제들 (python)
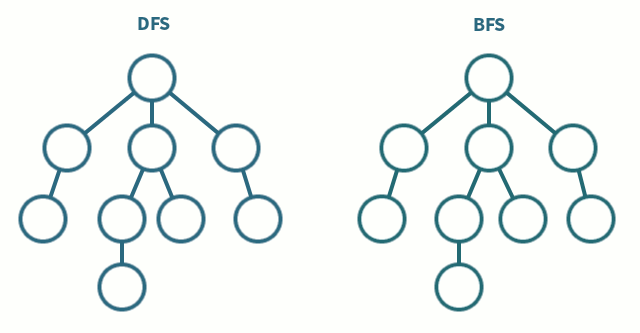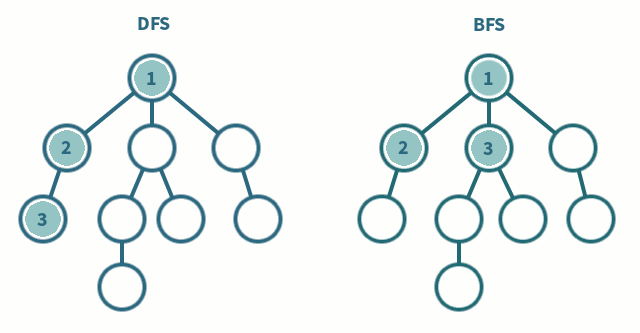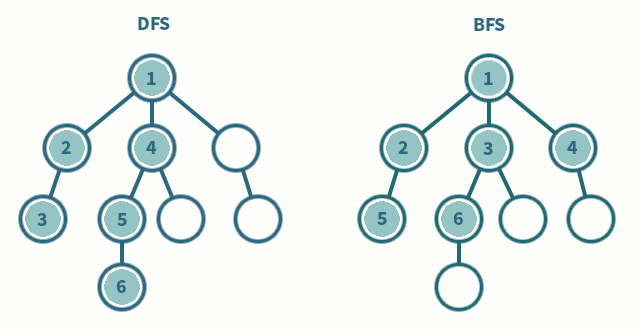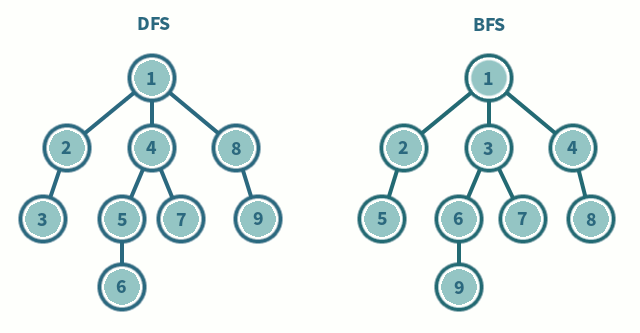
시작하기에 앞서..
그래프의 표현 방법
그래프는 표현하는 방법을 크게 두가지로 나눌 수 있습니다. 하나는 인접 행렬, 다른 하나는 인접 리스트입니다.
1. 인접 행렬 (Adjacency Matrix)
2차원 배열로 그래프의 연결관계를 표현하는 방식입니다.
INF = float('inf')
graph = [
[0, 7, 5],
[7, 0, INF],
[5, INF, 0]
]2. 인접 리스트 (Adjacency List)
리스트로 그래프의 연결관계를 표현하는 방식입니다. 저의 경우에는 딕셔너리나 collections에 있는 defaultdict를 사용합니다. 둘이 똑같이 키-값의 구조라서 빠른 접근이 가능하다는 점에서 사용하기 편리한 것 같습니다ㅎㅎ 아래는 defaultdict를 사용한 방법입니다.
graph = collections.defaultdict(list)
graph[0].append((i, j)) # 0번 노드와 i번 노드가 j의 거리로 연결되어 있다그래프 문제 자체가 TLE가 많이 날 수 있는 문제들을 직면할 가능성이 높은데, 그래서 인접행렬로 풀면 종종 안풀리는 경우들이 많더라구요. 개인적으로는 인접 행렬이 조금 더 편하다고 느껴지지만, 인접 리스트를 더 사용하는 방법이 좋을 것 같습니다!!
DFS
Depth First Search, 깊이 우선 탐색
트리나 그래프에서 한 루트로 계속 탐색하다가 다시 돌아와 다른 루트로 탐색하는 방식입니다. 대표적으로 _백트래킹_에 사용하며, 일반적으로 재귀호출을 사용하여 구현합니다. (단순 스택 배열로 구현하기도 합니다!) 구조상 스택 오버플로우를 조심해야한다는 특징이 있습니다. 적당한 조건에서 재귀를 끝내줘야하는 것이죠.
단순 검색 속도자체는 뒤에 나올 BFS에 비해 느립니다. 하지만 검색이 아닌 순회(traverse)를 할 경우에는 많이 쓰입니다. DFS는 특히 리프 노드에만 데이터를 저장하는 정렬 트리 구조에서 항상 순서대로 데이터를 방문한다는 장점이 있습니다.
여러가지 트리 순회 알고리즘

- 전위 순회 (preorder)
- 현재 노드 -> 왼쪽 트리 -> 오른쪽 트리 순서대로 방문하는 방법.
- 중위 순회 (Inorder)
- 왼쪽 트리 -> 현재 노드 -> 오른쪽 트리 순서대로 방문하는 방법
- 후위 순회 (Postorder)
- 왼쪽 트리 -> 오른쪽 트리 -> 현재 노드 순서대로 방문하는 방법
- 레벨 순서 순회 (level-order)
- 모든 노드를 낮은 레벨부터 차례대로 순회. (=BFS)
(예전에 면접볼때 나왔던 순회들... 이 사이트에 있는 슈도코드 정도는 알고가시면 좋을 것 같습니다!!)
동작 과정
스택 자료구조를 사용하여 DFS를 하는 방법을 한번 살펴봅시다.
- 탐색 노드를 스택에 삽입하고 방문 처리를 합니다.
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 있다면 그 인접 노드를 스택에 넣고 방문 처리를 합니다. 방문하지 않은 인접 노드가 없으면 최상단 노드를 꺼냅니다.
- 2번의 과정을 더이상 수행할 수 없을 때까지 반복합니다.
Python 코드
예제 코드를 한번 살펴봅시다. 매우 간단합니다
def dfs(graph, v, visited):
visited[v] = True
for i in graph[v]:
if not visited[i]:
dfs(graph, i, visited)
장단점
- 장점
- 현재 경로상의 노드들만 기억하면 되므로 저장 공간의 수요가 비교적 작다는 특징이 있습니다.
- 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있습니다.
- 단점
- 해가 없는 경로에 깊이 빠질 가능성이 있습니다.
- 얻어진 해가 최단 경로가 된다는 보장이 없습니다.
BFS
Breadth First Search, 너비 우선 탐색
BFS는 가까운 노드부터 탐색하는 알고리즘으로, DFS는 깊이를 우선적으로 탐색했다면 BFS는 그 반대입니다.
BFS에서는 선입선출 방식인 큐 자료구조를 사용하는 것이 정석으로, 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게되어 가까운 노드부터 탐색을 진행할 수 있습니다.
알고리즘 동작 방식
- 탐색 시작 노드를 큐에 삽입하고 방문 처리를 합니다.
- 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리를 합니다.
- 2번의 과정을 더이상 수행할 수 없을 때까지 반복합니다.
샘플 코드
BFS는 큐 자료구조에 기초한다는 점에서 구현이 간단합니다. 파이썬에서는 collections 모듈에 있는 deque 라이브러리를 사용하는것이 좋습니다. (그냥 리스트를 사용할 경우보다 훨씬 편합니다 ㅎㅎ) 일반적인 경우 실제 수행 시간은 DFS보다 좋은 편입니다.
from collections import deque
def bfs(graph, start, visited):
queue = deque([start])
visited[start] = True
while queue:
v = queue.popleft()
for i in graph[v]:
if not visitied[i]:
queue.append(i)
visitied[i] = True
관련 문제
DFS, BFS는 기업 코테에서 정말 자주 출제되는 유형인데요... 아주 기본 문제만 가져와보았습니다.
Leetcode 1765. Map of Highest Peak
Map of Highest Peak - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
주어진 그래프가 있고 물이 있는 영역의 높이는 0, 다른 부분은 서로 인접한 부분으로부터 1씩만 증가하는데 가장 높이가 높도록 설계하라는 문제입니다.
DFS로도 풀 수 있는 문제지만 TLE 에러가 납니다. BFS로 풀어주어야 하는 문제입니다!
Main Idea
- 높이를 기록하는 res 2차원 배열을 모두 0으로 초기화해줍니다.
- 먼저 큐에 물의 위치들과 높이(0)을 넣어줍니다.
- 큐를 하나씩 빼보면서 인접한 영역에 방문하지 않았으면 방문합니다. 인접한 영역 방문할 때 해당 노드의 높이에서 +1을 해줍니다.
- 마지막에 결과 res를 리턴해주면 끝!
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution:
def highestPeak(self, isWater: List[List[int]]) -> List[List[int]]:
m = len(isWater)
n = len(isWater[0])
res = [[0 for _ in range(n)] for _ in range(m)]
q = collections.deque([])
visited = set()
for i in range(m):
for j in range(n):
if isWater[i][j] == 1:
q.append([[i, j], 0])
visited.add((i, j))
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]
while q:
curr, value = q.popleft()
x, y = curr
for i, j in zip(dx, dy):
nx = x + i
ny = y + j
if 0 <= nx < m and 0 <= ny < n:
if (nx, ny) not in visited:
visited.add((nx, ny))
q.append([[nx, ny], value+1])
res[nx][ny] = value + 1
return res
|
cs |
Leetcode 994. rotting oranges
leetcode.com/problems/rotting-oranges/
썩은 오렌지가 있고 1초마다 인접 오렌지들을 썩게합니다. 모두 썩게할 수 있으면 모두 썩게하는데 몇초가 걸리는지를 리턴하고 그렇지 않으면 -1을 반환하는 문제입니다.
위의 문제랑 비슷합니다.. ㅎㅂㅎ 어째선지 다 이런 좌표찍는 문제들만 가져왔네요.
Main Idea
- 얼마나 시간이 걸리는지를 나타내는 graph 2차원 배열을 모두 -1로 초기화해줍니다.
- 썩은 오렌지가 있으면 해당 좌표의 graph 값을 0으로 하고 방문했다고 체크, 그리고 큐에 넣어줍니다.
- 큐를 하나씩 빼보면서 인접한 영역에 방문하지 않았고 신선한 오렌지면 방문 처리를 하고 시간을 기록해줍니다.
- 마지막에 하나씩 탐색하면서 신선한 오렌지의 영역인데 썩지 않았으면 -1을 리턴, 그렇지 않으면 걸린 최대 시간을 리턴해줍니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
class Solution:
def orangesRotting(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
q = collections.deque([])
visited = set()
graph = [[-1 for _ in range(n)] for _ in range(m)]
# 썩은 오렌지 찾기..
for i in range(m):
for j in range(n):
if grid[i][j] == 2:
q.append([[i, j], 0])
graph[i][j] = 0
visited.add((i, j))
dx = [-1, 0, 1, 0]
dy = [0, -1, 0, 1]
while q:
curr, value = q.popleft()
x, y = curr
for i, j in zip(dx, dy):
nx, ny = x + i, y + j
if 0 <= nx < m and 0 <= ny < n:
if (nx, ny) not in visited and grid[nx][ny] == 1:
visited.add((nx, ny))
q.append([[nx, ny], value+1])
graph[nx][ny] = value + 1
answer = 0
for i in range(m):
for j in range(n):
answer = max(answer, graph[i][j])
if grid[i][j] == 1 and graph[i][j] == -1:
return -1
return answer
|
cs |
지금까지 BFS, DFS에 대해서 살펴봤습니다. 저도 겸사겸사 정리하고.. ㅎㅎㅎㅎ 항상 그렇지만 BFS, DFS는 어떻게 풀어야겠다! 라는 생각이 정말 딱 바로 떠오르지만 막상 풀면 생각대로 안되는 경우가 많은 것 같습니다.
제 나름의 팁??이 있다면... 먼저 BFS로 도전하고 안되면 DFS, 효율성 통과를 못하면 memoization을 쓸 수 있으면 사용하는 방법.. 정도..? 물론 시간이 촉박하고 그러면 저도 잘 못하긴 하지만요 ㅎㅎㅎㅠㅠ
아무튼 DFS와 BFS에 대해서 알아보는 시간을 가졌습니다! 😆
'알고리즘 Algorithm ' 카테고리의 다른 글
| [Algorithm] 투포인터(Two Pointer) 알고리즘 (0) | 2021.04.28 |
|---|---|
| [Algorithm] 트라이(Trie)와 관련 문제들 (Python) (0) | 2021.04.11 |
| [Algorithm] 인프런 강좌 따라하며 배우는 알고리즘! 73장~75장 (0) | 2020.07.08 |
| [Algorithm] 인프런 강좌 따라하며 배우는 알고리즘! 72장 (0) | 2020.07.05 |
| [Algorithm] 인프런 강좌 따라하며 배우는 알고리즘! 70장 ~ (0) | 2020.07.03 |
댓글
이 글 공유하기
다른 글
-
[Algorithm] 투포인터(Two Pointer) 알고리즘
[Algorithm] 투포인터(Two Pointer) 알고리즘
2021.04.28 -
[Algorithm] 트라이(Trie)와 관련 문제들 (Python)
[Algorithm] 트라이(Trie)와 관련 문제들 (Python)
2021.04.11 -
[Algorithm] 인프런 강좌 따라하며 배우는 알고리즘! 73장~75장
[Algorithm] 인프런 강좌 따라하며 배우는 알고리즘! 73장~75장
2020.07.08 -
[Algorithm] 인프런 강좌 따라하며 배우는 알고리즘! 72장
[Algorithm] 인프런 강좌 따라하며 배우는 알고리즘! 72장
2020.07.05