[algorithm] 트리 - 트리의 구현과 순회
글 작성자: _rian
트리의 개념
트리는 노드로 이루어진 자료 구조
- 트리는 하나의 루트 노드를 갖는다.
- 루트 노드는 0개 이상의 자식 노드를 가지고 있다.
- 그 자식 노드 또한 0개 이상의 자식 노드를 가지고 있고, 이는 반복적으로 정의된다.
트리는 노드(node)들과 노드들을 연결하는 간선(edge)로 구성되어있다.
- 트리에는 사이클(cycle)이 존재할 수 없다.
- 노드들은 특정 순서로 나열될 수도 있고 그럴 수 없을 수도 있다.
- 각 노드는 부모 노드로의 연결이 있을수도 있고 없을 수도 있다.
- 각 노드는 어떤 자료형으로도 표현 가능하다.
class Node{ public String name; public Node[] children; } 비선형자료구조로 계층적 관계를 표현한다. ex) 디렉터리구조, 조직도- 그래프의 한 종류다.
- 사이클이 없는 하나의 연결 그래프
- 또는 DAG(Directed Acyclic Graph, 방향성이 있는 비순환 그래프)의 한종류이다.
트리와 관련된 용어
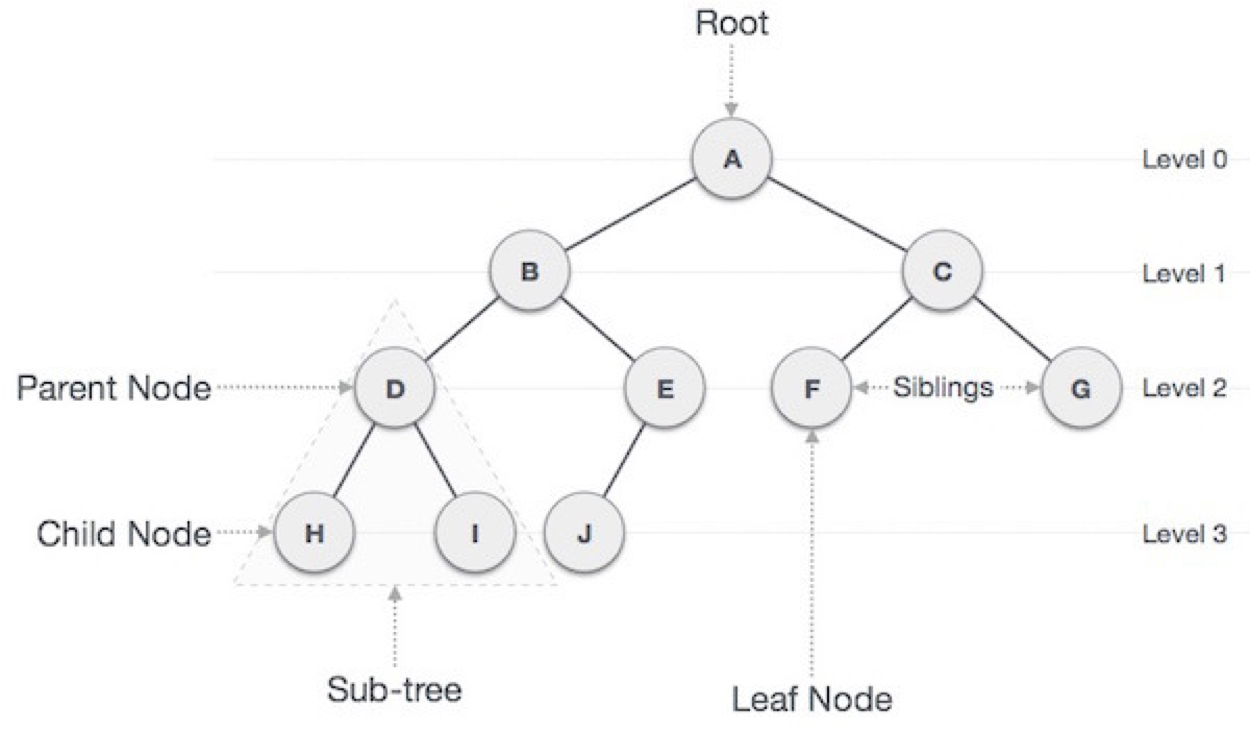
- 루트 노드 (root node) : 제일 최고 부모 노드. 트리는 하나의 루트노드만을 가진다.
- 단말 노드 (leaf node) : 자식이 없는 노드. '말단 노드' 또는 '잎 노드' 라고도 불린다.
- 내부 (internal) 노드 : 단말 노드가 아닌 노드
- 간선(edge) : 노드를 연결하는 선 (link, branch라고도 부른다.)
- 형제 (sibiling) : 같은 부모를 가지는 노드
- 노드의 크기 (size) : 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이 (depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야하는 간선의 수
- 노드의 레벨 (level) : 트리의 특정 깊이를 가지는 노드의 집합
- 노드의 차수 (degree) : 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
- 트리의 차수 (degree of tree) : 트리의 최대 차수
- 트리의 높이 (height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
트리(Tree)의 특징
- 그래프의 한 종류다.
최소 연결 트리라고도 불린다. - 트리는
계층 모델이다. - 트리는 DAG(Directed Acyclic Graphs, 방향성이 있는 비순환 그래프)의 한종류이다.
- loop나 circuit이 없다. 즉, 사이클이 없다.
- 노드가 N개인 트리는 항상
N-1개의 간선(edge)를 가진다. - 루트에서 어떤 노드로 가는 경로는 유일하다.
- 임의의 두 노드간의 경로도 유일하다.
- 한 개의 루트 노드만이 존재하며 모든 자식 노드는 한 개의 부모 노드만을 가진다.
- 순회는
Pre-order,In-order,Post-order로 이루어진다. 이 세가지 모두 DFS/BFS 안에 있다. - 트리는 이진트리, 이진탐색트리, 균형트리(AVL트리, red-black트리), 이진 힙(최대 힙, 최소 힙) 등이 있다.
트리(Tree)의 종류
이진트리
- 각 노드가 최대 두개의 자식을 가지는 트리
- 모든 트리가 이진트리는 아니다.
순회의 종류
순회는 재귀(Recursion)으로 구현한다!!
- 전위 순회 (pre-order traversal)
- 현재 노드 -> 왼쪽 가지 -> 오른쪽 가지
void preOrderTraversal(TreeNode node){ if(node != null){ visit(node); preOrderTraversal(node.left); preOrderTraversal(node.right); } }
- 중위 순회 (in-order traversal)
- 왼쪽 가지 -> 현재 노드 -> 오른쪽 가지
void inOrderTraversal(TreeNode node){ if(node!=null){ inOrderTraversal(node.left); visit(node); inOrderTraversal(node.right); } }
- 후위 순회 (post-order traversal)
- 왼쪽 가지 -> 오른쪽 가지 -> 현재 노드
void postOrderTraversal(TreeNode node){ if(node != null){ postOrderTraversal(node.left); postOrderTraversal(node.right); visit(node); } }
이진 탐색 트리 (Binary Search Tree)
- 모든 노드가 아래의 순서를따르는 속성이 있는 이진 트리다.
- 모든 노드 왼쪽 자식들 <= n < 모든 오른쪽 자식들 (모든 노드 n에 대해서 반드시 참)
균형 트리
- O(logN) 시간에 Insert와 find를 할 수 있을 정도로 균형이 잘 잡혀있는 경우
- ex) 레드-블랙 트리, AVL 트리
완전 이진 트리 vs 전 이진 트리 vs 포화 이진 트리
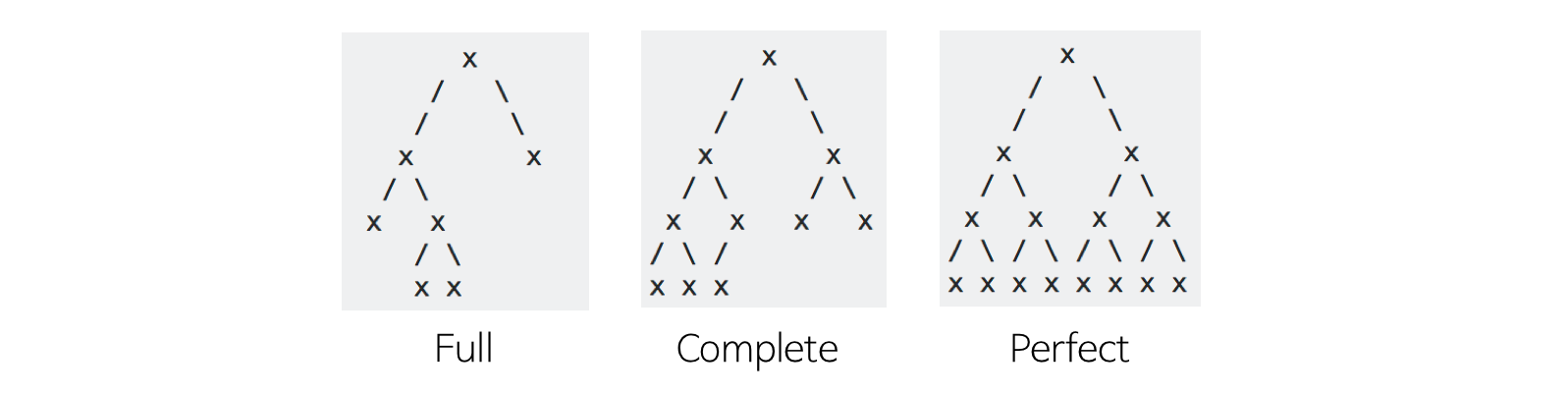
1. 완전 이진 트리 (Complete Binary Tree)
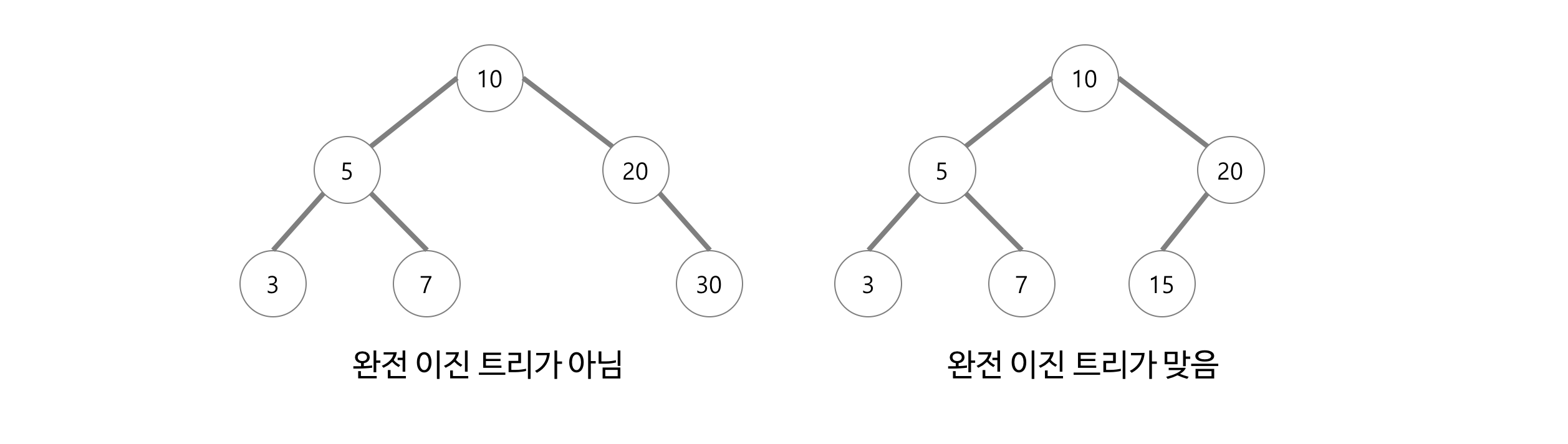
- 트리의 모든 높이에서 노드가 꽉 차있는 이진 트리. 즉, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져있다.
- 마지막 레벨은 꽉 차있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
- 마지막 레벨 h에서 (1 ~ 2h-1) 개의 노드를 가질 수 있다.
- 또 다른 정의는 가장 오른쪽 잎 노드가 (아마도 모두) 제거된 포화 이진 트리다.
- 완전 이진 트리는 배열을 사용해 효율적으로 표현 가능하다.
2. 전 이진트리 (Full Binary Tree 또는 Strictly Binary Tree)
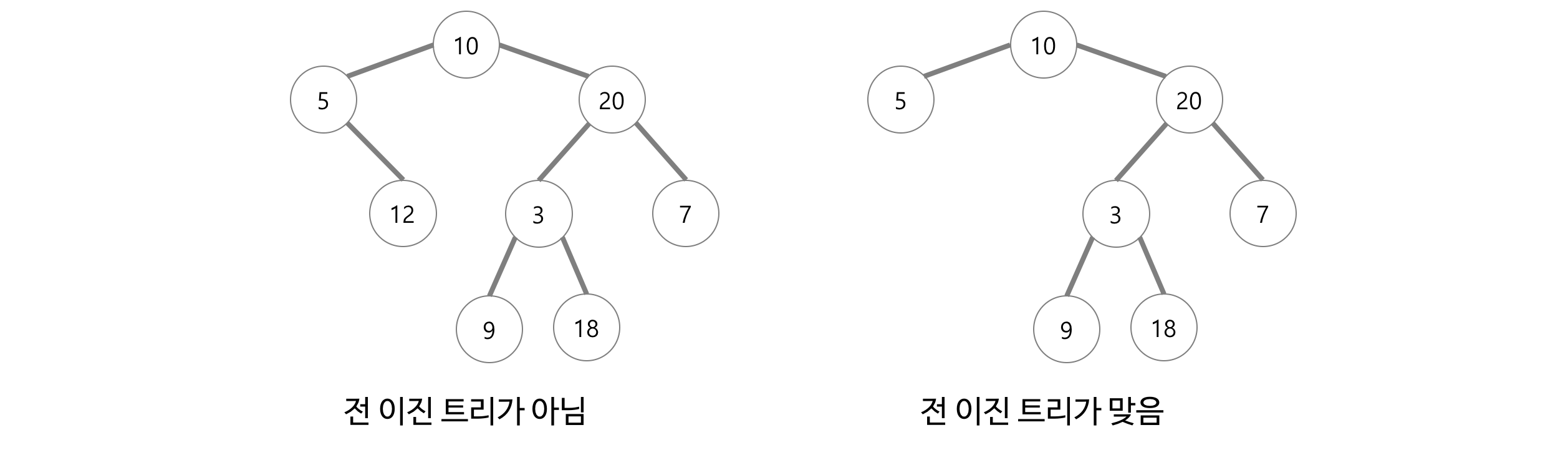
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
3. 포화 이진 트리 (Perfect Binary Tree)
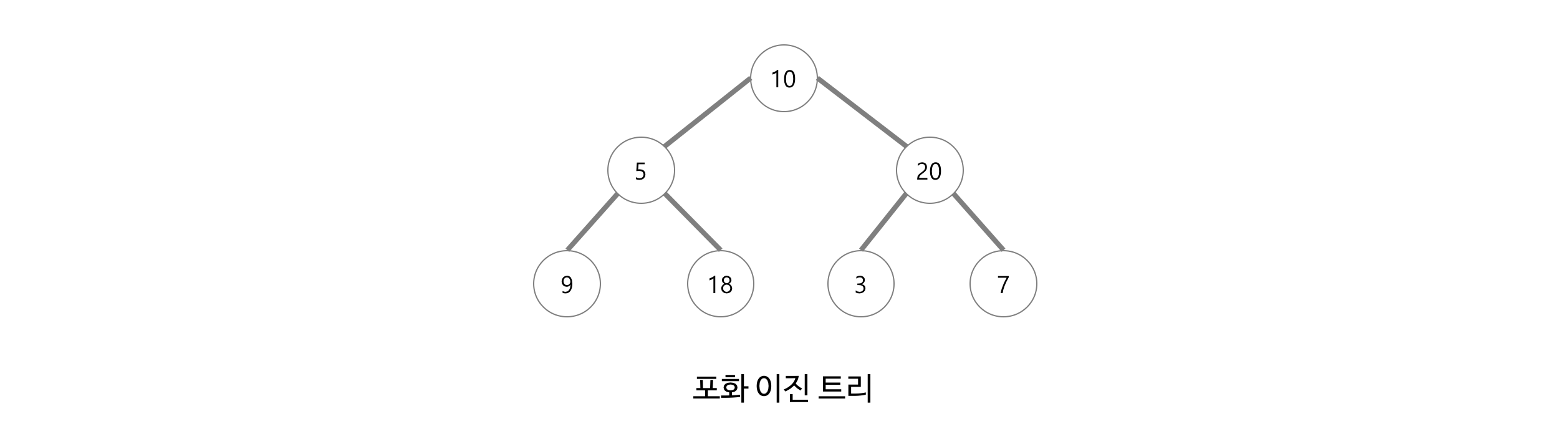
- 전 이진 트리이면서 완전 이진 트리인 경우
- 모든 말단 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 개수가 최대가 되어야 한다.
- 모든 내부 노드는 두 개의 자식 노드를 가진다.
- 모든 말단 노드가 동일한 깊이 또는 레벨을 갖는다.
- 노드의 개수가 정확히 2^(k-1)개여야 한다. (k : 트리의 높이) -> 흔하게 나타나는 경우가 아니다. 즉, 이진 트리가 모두 포화 이진 트리일 것이라고 생각하지 않는다.
이진 힙 (최소 힙과 최대 힙)
1. 최소 힙 (Min Heap)
- 트리의 마지막 단계에서 오른쪽 부분을 뺀 나머지 부분이 가득 채워져있는 완전 이진 트리이며, 각 노드의 원소가 자식들의 원소보다 작다.
- 즉, key(부모 노드) >= key(자식 노드)인 완전 이진 트리.
- 가장 큰 값은 루트 노드이다.
- N개가 힙에 들어가 있으면 높이는 log(N)이다.
2. 최대 힙 (Max Heap)
- 원소가 내림차순으로 정렬되어 있다는 점에서만 최소힙과 다르다.
- 각 노드의 원소가 자식들의 원소보다 크다.
트라이(Trie ; '접두사 트리(Prefix Tree'라고도 부른다.)
- n차 트리(n-ary Tree)의 변종
- 각 노드에 문자를 저장하는 자료구조
- 따라서 트리를 아래쪽으로 순회하면 단어 하나가 나온다.
- 접두사를 빠르게 찾아보기 위한 흔한 방식으로, 모든 언어를 트라이에 저장해 놓는 방식이 있다.
- 유효한 단어 집합을 이용하는 많은 문제들은 트라이를 통해 최적화할 수 있다.
트리(Tree)의 구현 방법
기본적으로 트리는 그래프의 한 종류이므로 구현 방법(인접 리스트 또는 인접 배열)으로 구현할 수 있다.
1. 인접 배열 이용
- 1차원 배열에 자신의 부모노드만 저장하는 방법
- 트리는 부모 노드를 0개 또는 1개를 가지기 때문
- 부모 노드를 0개 : 루트 노드
- 이진 트리의 경우, 2차원 배열에 자식 노드를 저장하는 방법
- 이진 트리는 각 노드가 최대 두 개의 자식을 갖는 트리이기 때문
- ex) A[i][0] : 왼쪽 자식 노드, A[i][1] : 오른쪽 자식 노드
2. 인접 리스트 이용
- 가중치가 없는 트리의 경우
ArrayList<ArrayList> list = new ArrayList<>();
- 가중치가 있는 트리의 경우
- 1)
class Node {int num, dist; //노드 번호, 거리}정의 - 2)
ArrayList[] list = new ArrayList[정점의 수 + 1];
- 1)
그래프의 트리의 차이
| 구분 | 그래프 | 트리 |
|---|---|---|
| 정의 | 노드(node)와 그 노드를 연결하는 간선(edge)를 하나로 모아높은 자료 구조 | 그래프의 한 종류. DAG(Directed Acylic Graph, 방향성이 있는 비순환 그래프)의 한 종류 |
| 방향성 | 방향 그래프(Directed), 무방향 그래프(Undirected) 모두 존재함. | 방향 그래프(Directed Graph) |
| 사이클 | 사이클(cycle) 가능 자체 간선(self loop) 가능 순환 그래프(cyclic), 비순환 그래프 (acyclic) 모두 존재. | 사이클 불가능 자체 간선도 불가능 비순환 그래프 |
| 루트 노드 | 루트 노드의 개념이 없음. | 한 개의 루트 노드만이 존재. 모든 자식 노드는 한 개의 부모 노드만을 가짐. |
| 부모 - 자식 | 부모 - 자식의 개념이 없음. | 부모-자식 관계. top-bottom 또는 Bottom-up 으로 이루어짐. |
| 모델 | 네트워크 모델 | 계층 모델 |
| 순회 | DFS, BFS | DFS, BFS 안의 Pre-, In-, Post- Order |
| 간선의 수 | 그래프에 따라 간선의 수가 다름. 간선이 없을 수도 있음. | 노드가 N인 트리는 항상 N-1의 간선을 가짐. |
| 경로 | - | 임의의 두 노드간의 경로는 유일 |
| 예시 및 종류 | 지도, 지하철 노선도의 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방 통행길), 선수과목 | 이진트리, 이진 탐색 트리 균형 트리(AVL 트리, red-block 트리), 이진 힙(최대 힙, 최소 힙) 등 |
Reference
'알고리즘 Algorithm ' 카테고리의 다른 글
| [Algorithm] 따라하며 배우는 인프런 강좌! 6강~10강 (0) | 2020.06.10 |
|---|---|
| [algorithm] 그래프의 개념과 정의, 탐색 방법 (0) | 2019.12.01 |
| Kick Start 2019 Round H 후기 (0) | 2019.11.17 |
| 구글의 온라인 알고리즘 대회, Kick Start (0) | 2019.11.12 |
| 선형 자료구조 - 큐, 스택, 데크 (0) | 2019.11.01 |
댓글
이 글 공유하기
다른 글
-
[Algorithm] 따라하며 배우는 인프런 강좌! 6강~10강
[Algorithm] 따라하며 배우는 인프런 강좌! 6강~10강
2020.06.10 -
[algorithm] 그래프의 개념과 정의, 탐색 방법
[algorithm] 그래프의 개념과 정의, 탐색 방법
2019.12.01 -
Kick Start 2019 Round H 후기
Kick Start 2019 Round H 후기
2019.11.17 -
구글의 온라인 알고리즘 대회, Kick Start
구글의 온라인 알고리즘 대회, Kick Start
2019.11.12


